2.5 - Multiple (pair-wise) comparisons using Tukey's HSD and the compact letter display
by
With evidence that the true means are likely not all equal, many researchers want to know which groups show evidence of differing from one another. This provides information on the source of the overall difference that was detected and detailed information on which groups differed from one another. Because this is a shot-gun/ unfocused sort of approach, some people think it is an over-used procedure. Others feel that it is an important method of addressing detailed questions about group comparisons in a valid way. For example, we might want to know if OJ is different from VC at the 0.5 mg dosage level and these methods will allow us to get an answer to this sort of question. It also will test for differences between the OJ-0.5 and VC-2 groups and every other pair you can construct. This method actually takes us back to the methods in Chapter 1 where we compared the means of two groups except that we need to deal with potentially many pair-wise comparisons, making an adjustment to account for that inflation in Type I errors that occurs due to many tests being performed at the same time. There are many different statistical methods to make all the pair-wise comparisons, but we will employ the most commonly used one, called Tukey's Honest Significant Difference (Tukey's HSD) method28 . The name suggests that not using it could lead to a dishonest answer and that it will give you an honest result. It is more that if you don't do some sort of correction for all the tests you are performing, you might find some spurious29 results. There are other methods that could be used to do a similar correction.
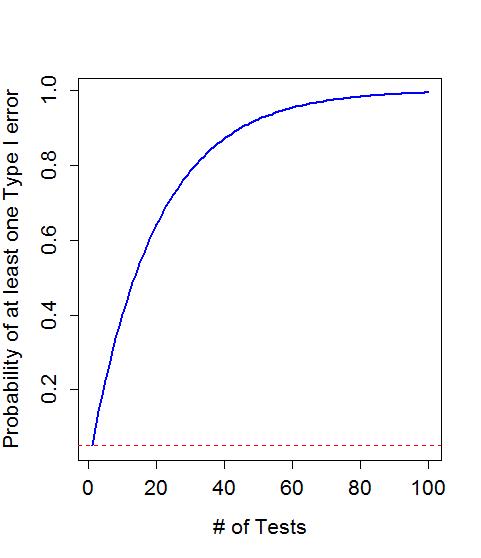
Generally, the general challenge in this situation is that if you perform many tests at the same time, you inflate the Type I error rate. We can define the family-wise error rate as the probability that at least one error is made on a set of tests or P(At least 1 error is made). The family-wise error is meant to capture the overall situation in terms of measuring the likelihood of making a mistake if we consider many tests, each with some chance of making their own mistake, and focus on how often we make at least one error when we do many tests. A quick probability calculation shows the magnitude of the problem. If we start with a 5% significance level test, then P(Type I error on one test) =0.05 and the P(no errors made on one test) =0.95, by definition. This is our standard hypothesis testing situation. Now, suppose we have m independent tests, then P(make at least 1 Type I error given all null hypotheses are true) = 1 - P(no errors made) = 1 - .95m. Figure 2-17 shows how the probability of having at least one false detection grows rapidly with the number of tests. The plot stops at 100 tests since it is effectively a 100% chance of at least on false detection. It might seem like doing 100 tests is a lot, but in Genetics research it is possible to consider situations where millions of tests are considered so these are real issues to be concerned about in many situations.
In pair-wise comparisons between all the pairs of means in a One-Way ANOVA, the number of tests is based on the number of pairs. We can calculate the number of tests using J choose 2, (J2), to get the number of pairs of size 2 that we can make out of J individual treatment levels. We won't explore the combinatorics formula for this, as the choose function can give us the answers:
> choose(3,2)
[1] 3
> choose(4,2)
[1] 6
> choose(5,2)
[1] 10
> choose(6,2)
[1] 15
So if you have 6 groups, like in the Guinea Pig study, we will have to consider 15 tests to compare all the pairs of groups. 15 tests seems like enough that we should be worried about inflated family-wise error rates. Fortunately, the Tukey's HSD method controls the family-wise error rate at your specified level (say 0.05) across any number of pair-wise comparisons. This means that the overall rate of at least one Type I error is controlled at the specified significance level, often 5%. To do this, each test must use a slightly more conversative cut-off than if just one test is performed and the procedure helps us figure out how much more conservative we need to be.
Tukey's HSD starts with focusing on the difference between the groups with the largest and smallest means (γ̅max -γ̅min). If (γ̅max - γ̅min) ≤ Margin of Error for the difference in the means, then all other pairwise differences, say |γ̅j - γ̅j'|, will be less than or equal to that margin of error. This also means that any confidence intervals for any difference in the means will contain 0. Tukey's HSD selects a critical value so that (γ̅max - γ̅min) will be less than the margin of error in 95% of data sets drawn from populations with a common mean. This implies that in 95% of datasets in which all the population means are the same, all confidence intervals for differences in pairs of means will contain 0. Tukey's HSD provides confidence intervals for the difference in true means between groups j and j', μj - μj', for all pairs where j ≠ j', using
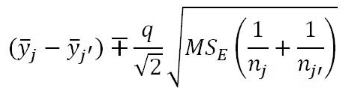
where 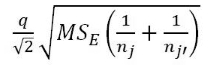 is the margin of error for the intervals. The distribution used to find the multiplier, q, for the confidence intervals is available in the qtukey function and generally provides a slightly larger multiplier than the regular t* from our two-sample t-based confidence interval, discussed in Chapter 1. We will use the confint, cld, and plot functions applied to output from the glht function (multcomp package; Hothorn, Bretz and Westfall, 2008) to easily get the required comparisons from our ANOVA model. Unfortunately, its code format is a little complicated - but there are just two places to modify the code, by including the modele name and after mcp (stands for multiple comparisons) in the linfct option, you need to include the explanatory variable name as VARIABLENAME="Tukey". The last part is to get the Tukey HSD multiple comparisons. Once we obtain the intervals, we can use them to test H0: γj = γj' vs HA: γj ≠ γj' by assessing whether 0 is in the confidence for each pair. If 0 is in the interval, then there is no evidence of a difference for that pair. If 0 is not in the interval, then we reject H0 and have evidence at the specified family-wise significance level of a difference for that pair. The following code provides the numerical and graphical30 results of applying Tukey's HSD to the linear model for the Guinea Pig data:
is the margin of error for the intervals. The distribution used to find the multiplier, q, for the confidence intervals is available in the qtukey function and generally provides a slightly larger multiplier than the regular t* from our two-sample t-based confidence interval, discussed in Chapter 1. We will use the confint, cld, and plot functions applied to output from the glht function (multcomp package; Hothorn, Bretz and Westfall, 2008) to easily get the required comparisons from our ANOVA model. Unfortunately, its code format is a little complicated - but there are just two places to modify the code, by including the modele name and after mcp (stands for multiple comparisons) in the linfct option, you need to include the explanatory variable name as VARIABLENAME="Tukey". The last part is to get the Tukey HSD multiple comparisons. Once we obtain the intervals, we can use them to test H0: γj = γj' vs HA: γj ≠ γj' by assessing whether 0 is in the confidence for each pair. If 0 is in the interval, then there is no evidence of a difference for that pair. If 0 is not in the interval, then we reject H0 and have evidence at the specified family-wise significance level of a difference for that pair. The following code provides the numerical and graphical30 results of applying Tukey's HSD to the linear model for the Guinea Pig data:
> require(multcomp)
> Tm2 <- glht(m2, linfct = mcp(Treat = "Tukey"))
> confint(Tm2)
Simultaneous Confidence Intervals
Multiple Comparisons of Means: Tukey Contrasts
Fit: lm(formula = len ~ Treat, data = ToothGrowth)
Quantile = 2.9549
95% family-wise confidence level
| Linear Hypotheses: | |||
| Estimate | lwr | upr | |
| VC.0.5 - OJ.0.5 == 0 | -5.2500 | -10.0487 | -0.4513 |
| OJ.1 - OJ.0.5 == 0 | 9.4700 | 4.6713 | 14.2687 |
| VC.1 - OJ.0.5 == 0 | 3.5400 | -1.2587 | 8.3387 |
| OJ.2 - OJ.0.5 == 0 | 12.8300 | 8.0313 | 17.6287 |
| VC.2 - OJ.0.5 == 0 | 12.9100 | 8.1113 | 17.7087 |
| OJ.1 - VC.0.5 == 0 | 14.7200 | 9.9213 | 19.5187 |
| VC.1 - VC.0.5 == 0 | 8.7900 | 3.9913 | 13.5887 |
| OJ.2 - VC.0.5 == 0 | 18.0800 | 13.2813 | 22.8787 |
| VC.2 - VC.0.5 == 0 | 18.1600 | 13.3613 | 22.9587 |
| VC.1 - OJ.1 == 0 | -5.9300 | -10.7287 | -1.1313 |
| OJ.2 - OJ.1 == 0 | 3.3600 | -1.4387 | 8.1587 |
| VC.2 - OJ.1 == 0 | 3.4400 | -1.3587 | 8.2387 |
| OJ.2 - VC.1 == 0 | 9.2900 | 4.4913 | 14.0887 |
| VC.2 - VC.1 == 0 | 9.3700 | 4.5713 | 14.1687 |
| VC.2 - OJ.2 == 0 | 0.0800 | -4.7187 | 4.8787 |
> old.par <- par(mai=c(1.5,2,1,1)) #Makes room on the plot for the group names
> plot(Tm2)
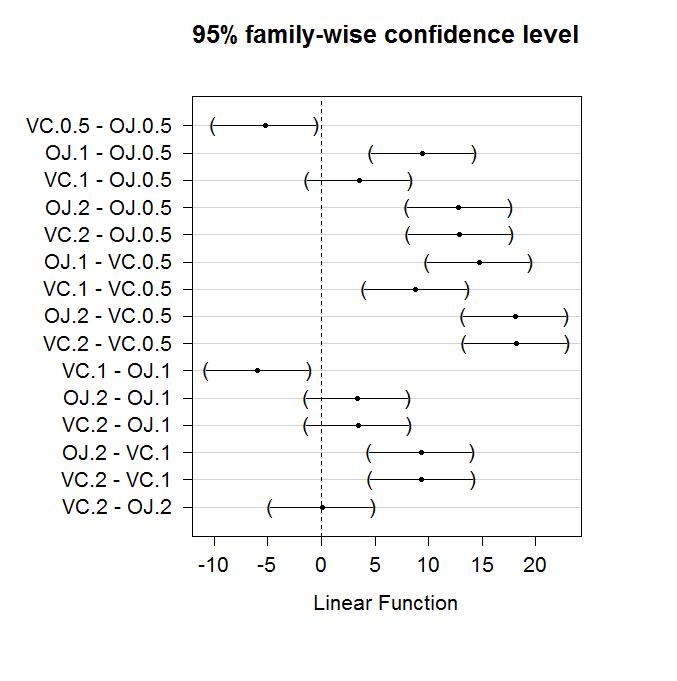
Figure 2-18 contains confidence intervals for the difference in the means for all 15 pairs of groups. For example, the first confidence interval in the first row is comparing VC.0.5 and OJ.0.5 (VC.0.5 minus OJ.0.5). In the numerical output, you can find that this 95% family-wise confidence interval goes from -10.05 to -0.45 mm (lwr and upr in the numerical output provide the CI endpoints). This interval does not contain 0 since its upper end point is -0.45 mm and so we can now say that there is evidence that OJ and VC have different true mean growth rates at the 0.5 mg dosage level. We can go further and say that we are 95% confident that the difference in the true mean tooth growth between VC0.5 and OJ0.5 (VC0.5-OJ0.5) is between -10.05 and -0.45 mm. But there are fourteen more similar intervals...
If you put all these pair-wise tests together, you can generate an overall interpretation of Tukey's HSD results that discusses sets of groups that are not detectably different from one another and those groups distinguished from other sets of groups. To do this, start with listing out the groups that do are not detectably different (CIs contain 0), which, here, only occurs for four of the pairs. The CIs that contain 0 are for the pairs VC.1 and OJ.0.5, OJ.2 and OJ.1, VC.2 and OJ.1, and, finally, VC.2 and OJ.2. So VC.2, OJ.1, and OJ.2 are all not detectably different from each other and VC.1 and OJ.0.5 are also not detectably different. If you look carefully, VC.0.5 is detected as different from every other group. So there are basically three sets of groups that can be grouped together as "similar": VC.2, OJ.1, and OJ.2; VC.1 and OJ.0.5; and VC.0.5. Sometimes groups overlap with some levels not being detectably different from other levels that belong to different groups and the story is not as clear as it is in this case. An example of this sort of overlap is seen in the next section.
There is a method that many researchers use to more efficiently generate and report these sorts of results that is called a compact letter display (CLD). The cld function can be applied to the results from glht to provide a "simple" summary of the sets of groups that we generated above. In this discussion, we are using a set as a union of different groups that can contain one or more members and the member of these groups are the six different treatment levels.
> cld(Tm2)
| OJ.0.5 | VC.0.5 | OJ.1 | VC.1 | OJ.2 | VC.2 |
| "b" | "a" | "c" | "b" | "c" | "c" |
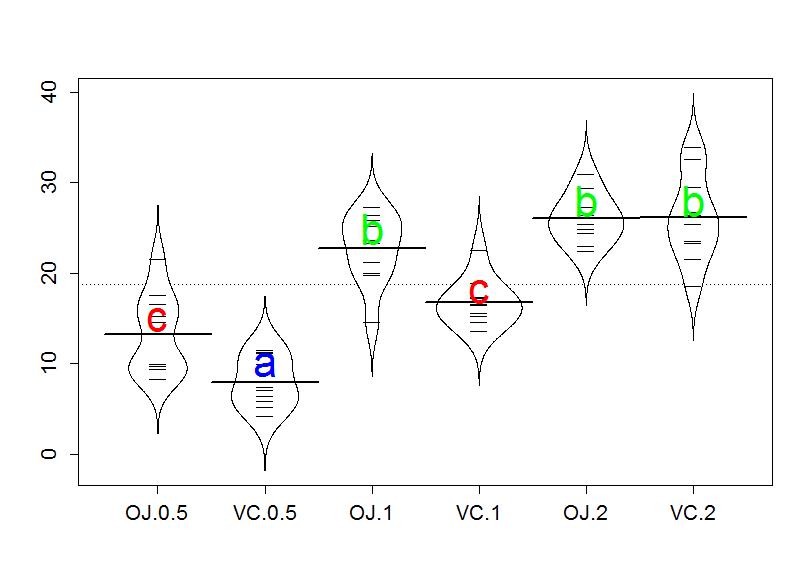
Groups with the same letter are not detectably different (are in the same set) and groups that are detectably different get different letters (different sets). Groups can have more than one letter to reflect "overlap" between the sets of groups and sometimes a set of groups contains only a single treatment level (VC.0.5 is a set of size 1). Note that if the groups have the same letter, this does not mean they are the same, just that there is no evidence of a difference for that pair. If we consider the previous output for the CLD, the "a" set contains VC.0.5, the "b" set contains OJ.0.5 and VC.1, and the "c" set contains OJ.1, OJ.2, and VC.2. These are exactly the groups of treatment levels that we obtained by going through all fifteen pairwise results. And these letters can be added to a beanplot to help fully report the results and understand the sorts of differences Tukey's HSD can detect.
> beanplot(len~Treat,data=ToothGrowth,log="",col="white",method="jitter")
> text(c(2),c(10),"a",col="blue",cex=2)
> text(c(3,5,6),c(25,28,28),"b",col="green",cex=2)
> text(c(1,4),c(15,18),"c",col="red",cex=2)
Figure 2-19 can be used to enhance the discussion by showing that the "a" group with VC.0.5 had the lowest average tooth growth, the "c" group had intermediate tooth growth for treatments OJ.0.5 and VC.1, and the highest growth rates came from OJ.1, OJ.2, and VC.2. Even though VC.2 had the highest average growth rate, we are not able to prove that its true mean is any higher than the other groups labeled with "b". Hopefully the ease of getting to the story of the Tukey's HSD results from a plot like this explains why it is common to report results using these methods instead of reporting 15 confidence intervals.
There are just a couple of other details to mention on this set of methods. First, note that we interpret the set of confidence intervals simultaneously: We are 95% confident that ALL the intervals contain the respective differences in the true means (this is a family-wise interpretation). These intervals are adjusted (wider) from our regular 2 sample t intervals from Chapter 1 to allow this stronger interpretation. Second, if sample sizes are unequal in the groups, Tukey's HSD is conservative and provides a family-wise error rate that is lower than the nominal level. In other words, it fails less often than expected and the intervals provided are a little wider than needed, containing all the pairwise differences at higher than the nominal confidence level of (typically) 95%. Third, this is a parametric approach and violations of normality and constant variance will push the method in the other direction, potentially making the technique dangerously liberal. Nonparametric approaches to this problem are possible, but will not be considered here.
28When this procedure is used with unequal group sizes it is also sometimes called Tukey-Kramer's method.
29We often use "spurious" to describe falsely rejected null hypotheses which are also called false detections.
30The plot of results usually contains all the labels of groups but if the labels are long or there many groups, sometimes the row labels are hard to see even with re-sizing the plot to make it taller in R-studio and the numerical output is useful as a guide to help you read the plot.