1.8a - Bootstrap confidence interval for difference in GPAs
by
We can now repeat the methods on the STAT 217 grade data. This time we can start with the parametric 95% confidence interval "by hand" and then using t.test. The favstats output provides us with the required information to do this ourselves:
favstats(GPA~Sex,data=s217)
| .group | min | Q1 | median | Q3 | max | mean | sd | n | missing | |
| 1 | F | 2.50 | 3.1 | 3.400 | 3.70 | 4 | 3.338378 | 0.4074549 | 37 | 0 |
| 2 | M | 1.96 | 2.8 | 3.175 | 3.46 | 4 | 3.088571 | 0.4151789 | 42 | 0 |
The df are 37+42-2 = 77. Using the SDs from the two groups and their sample sizes, we can calculate sp:
> sp=sqrt(((37-1)*(0.4075^2)+(42-1)*(0.41518^2))/(37+42-2))
> sp
[1] 0.4116072
The margin of error is:
> qt(.975,df=77)*sp*sqrt(1/37+1/42)
[1] 0.1847982
All together, the 95% confidence interval is:
> 3.338-3.0886+c(-1,1)*qt(.975,df=77)*sp*sqrt(1/37+1/42)
[1] 0.0646018 0.4341982
So we are 95% confident that the difference in the true mean GPAs between females and males (femals minus males) is between 0.065 and 0.434 GPA points. We get a similar20 result from the bolded part of the t.test output:
> t.test(GPA~Sex,data=s217,var.equal=T)
Two Sample t-test
data: GPA by Sex
t = 2.6919, df = 77, p-value = 0.008713
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.06501838 0.43459552
sample estimates:
| mean in group F | mean in group M |
| 3.338378 | 3.088571 |
Note that we can easily switch to 90% or 99% confidence intervals by simply changing the percentile in qt or changing conf.level in the t.test function. In the following two lines of code, we added hashtags (#) and then some text to explain what is being calculated. Hashtags provide a way of adding comments to R code as R will ignore any text after a hashtag on a given line.
> qt(.95,df=77) #For 90% confidence and 77 df
1] 1.664885
> qt(.995,df=77) #For 99% confidence and 77 df
[1] 2.641198
t.test(GPA~Sex,data=s217,var.equal=T,conf.level=.90)
t = 2.6919, df = 77, p-value = 0.008713
alternative hypothesis: true difference in means is not equal to 0
90 percent confidence interval:
0.09530553 0.40430837
> t.test(GPA~Sex,data=s217,var.equal=T,conf.level=.99)
t = 2.6919, df = 77, p-value = 0.008713
alternative hypothesis: true difference in means is not equal to 0
99 percent confidence interval:
0.004703598 0.494910301
As a review of some basic ideas with confidence intervals make sure you can answer the following questions:
- 1) What is the impact of increasing the confidence level in this situation?
- 2) What happens to the width of the confidence interval if the size of the SE increases or decreases?
- 3) What about increasing the sample size - should that increase or decrease the width of the interval?
All of the general results you learned before about impacts to widths of CIs hold in this situation whether we are considering the parametric or bootstrap methods.
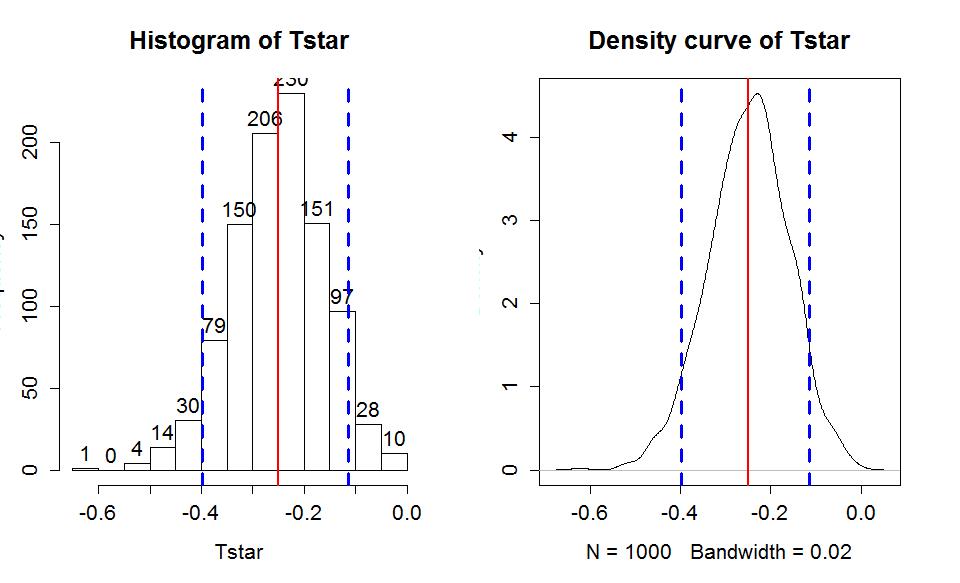
To finish this example, we will generate the comparable bootstrap 90% confidence interval using the bootstrap distribution in Figure 1-20.
> Tobs <- compareMean(GPA ~ Sex, data=s217); Tobs
[1] -0.2498069
> par(mfrow=c(1,2))
> B<- 1000
> Tstar<-matrix(NA,nrow=B)
> for (b in (1:B)){
+ Tstar[b]<-compareMean(GPA ~ Sex, data=resample(s217))
+ }
> qdata(.05,Tstar)
| p | quantile |
| 0.0500000 | -0.3974425 |
> qdata(.95,Tstar)
| p | quantile |
| 0.9500000 | -0.1147324 |
> quantiles<-qdata(c(.05,.95),Tstar)
> quantiles
| quantile | p | |
| 5% | -0.3974425 | 0.05 |
| 95% | -0.1147324 | 0.95 |
The output tells us that the 90% confidence interval is from -0.397 to -0.115 GPA points. The bootstrap distribution with the observed difference in the sample means and these cut-offs is displayed in Figure 1-20 using this code:
> hist(Tstar,labels=T)
> abline(v=Tobs,col="red",lwd=2)
> abline(v=quantiles$quantile,col="blue",lwd=3,lty=2)
> plot(density(Tstar),main="Density curve of Tstar")
> abline(v=Tobs,col="red",lwd=2)
> abline(v=quantiles$quantile,col="blue",lwd=3,lty=2)
In the previous output, the parametric 90% confidence interval is from 0.095 to 0.404, suggesting similar results again from the two approaches once you account for the two different orders of differencing. There was a slight left skew in the bootstrap distribution with one much smaller difference observed which generated some of the observed difference in the results. Based on the bootstrap CI, we can say that we are 90% confident that the difference in the true mean GPAs for STAT 217 students is between -0.397 to -0.115 GPA points (male minus females). Because sex cannot be assigned to the subjects, we cannot infer that sex is causing this difference and because this was a voluntary response sample of STAT 217 students in a given semester, we cannot infer that a difference of this size would apply to all STAT 217 students or even students in another semester.
Throughout the semester, pay attention to the distinctions between parameters and statistics, focusing on the differences between estimates based on the sample and inferences for the population of interest in the form of the parameters of interest. Remember that statistics are summaries of the sample information and parameters are characteristics of populations (which we rarely know). And that our inferences are limited to the population that we randomly sampled from, if we randomly sampled.
20We rounded the means a little and that caused the small difference in results.